문제
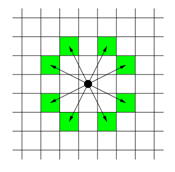
체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?
입력
입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.
각 테스트 케이스는 세 줄로 이루어져 있다. 첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다. 체스판의 크기는 l × l이다. 체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다. 둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.
출력
각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.
문제를 보고 얻어야 하는 인사이트
- 나이트가 이동할 수 있는 경로는 총 여덞 가지이다. [(X±2, Y±1), (X±1, Y±2)]
- 최솟값을 구하는 문제이기 때문에 경로 탐색을 하면서 노드별로 최솟값을 저장해가면서 풀어야한다.
- 같은 좌표로 가려고 할 경우에 대한 예외처리를 해야한다.
풀이 (BFS)
from collections import deque
# 나이트가 이동할 수 있는 경로
dx = [+1,-1,+1,-1,-2,-2,+2,+2]
dy = [+2,+2,-2,-2,+1,-1,+1,-1]
dimension = 0
visited = []
T = int(input())
def bfs(x, y):
queue = deque([[x,y]])
while queue:
x,y = queue.popleft()
# print(x, y)
# 문제에서 제시한 전체 여덞 경로 탐색
for i in range(8):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < dimension and 0 <= ny < dimension:
if visited[nx][ny] == 0: # 처음 방문하는 거라면
visited[nx][ny] = (visited[x][y] + 1)
queue.append([nx, ny])
else: # 이미 방문한 적이 있다면 기존 값과 비교해서 그 중 최소값인 수로 취한다.
visited[nx][ny] = min(visited[nx][ny], (visited[x][y] + 1))
for _ in range(T):
dimension = int(input())
visited = [[0] * dimension for _ in range(dimension)]
start_x, start_y = map(int, input().split())
target_x, target_y = map(int, input().split())
# 타겟 좌표와 같은 좌표라면 '0'
if start_x == target_x and start_y == target_y:
print(0)
else:
bfs(start_x, start_y)
# 최종 목적지에 도달하기 위한 최소 경로 출력
print(visited[target_x][target_y])
문제를 풀면서 느낀점
- 최솟값을 푸는 그래프 문제는 그래프 탐색 시 초기 조건을 반드시 달아주어야 한다. 초기 조건을 달아주지 않으면 계속 초기값을 최솟값으로 판단해서 의도하지 않은 값으로 풀이를 하게 되기 때문이다.